Citation with persistent identifier:
Smith, Neel. “Two Thousand Years of Scholarly Apps.” CHS Research Bulletin 4, no. 2 (2016). http://nrs.harvard.edu/urn-3:hlnc.essay:SmithN.Two_Thousand_Years_of_Scholarly_Apps.2016
https://youtu.be/6TwXYHdUiCY
Introduction
1§1 What does it mean to edit a text? This is obviously a foundational question for any literary or historical discipline that depends on the study of historical documents, but it has taken on a new urgency for editors grappling with the implications of digital information technology.
1§2 The long history of editing Greek texts can offer helpful perspective. In this paper, I consider a textual phenomenon unique to Greek scholarly writing, tables (κανόνες). Their use reflects the shared practices, language and habits of thought of a scholarly community, as the appearance of tables in distinctively scholarly textual genres would suggest. It also reveals how ancient authors and editors discovered in the technology of writing unique opportunities to respond to the needs of scholarly editions. The different forms of reading and functional interaction that tabular structures make possible enabled ancient scholars to express aspects of their work that were impossible to represent in prose. Considering how and why they organized scholarly material in tabular structures highlights some direct parallels to the choices that editors today must make. We, too, must organize our editions in structures that best express the meaning of an edition using the technologies available to us.
1§3 In this paper, I will first look at how the use of tables by Claudius Ptolemy and in other scholarly works including the term “Tables” (κανόνες) in their title can help us understand what I will call “functional editions” of texts. Finally, I will present possible approaches to digital editions of scholarly texts that take account of essential differences between these “functional editions” and editions of linear texts.
1. “Functional editions” in ancient Greek scholarship
2§1 Human beings have a unique capacity for working with systems of abstract symbols, and no illustration is more striking than our innate ability to learn languages. An English child formulates an expression like “It’s going to rain” using a present progressive form of a verb complemented by an infinitive as effortlessly as a Turkish child produces the correct agglutination “Yağmur yağacak” (or even “Yağmur yağacakmış” to add a nuance distancing the speaker from the assertion that is impossible to capture fully in English). Over the past five millennia, however, the development at various times of writing systems to represent language is an extraordinary achievement: the conscious invention of one system of symbols (a writing system) to represent another system of symbols (language). Without writing, language requires direct interaction of two or more people in the same place at the same time. Writing instead represents language by means of physical artifacts that can efface limits of time and space.
2§2 Writing also changes the strictly sequential experience of language that is inevitable in speech. Writing can of course define a sequential text: when we learn a writing system, we learn how to order its symbols (left to right, top to bottom, boustrophedon…) But written texts invite other sequences of reading. In the codex form of the modern book, readers can turn to the last page to find the guilty party in a murder mystery, or skip over a long argument and pass directly to a conclusion.
2§3 Paging column by column through a scroll is more cumbersome, but even a single page of a book or column of a volumen has the potential for different orderings. Hellenistic poets were keenly aware of the interplay of text and artifact when they composed “pattern poems,” and could also offer reorderings of the text in the form of acrostics, in which reading initial letters or syllables of poetic lines forms words or phrases.[1]
2§4 Hellenistic scholars similarly recognized that the spatial organization of a page could provide for a kind of non-linear reading in the form of the κανών, or table. Rather than challenging readers with puzzles, however, they created a means of looking up information by a key value. The mathematical term for this relation between a set of values in a given domain (the keys to the table) and resulting values in some range (the value that is looked up) is a function, and I will use the phrase “functional editions” to refer to scholarly texts incorporating functions, in this mathematical sense.
“Functional editions” in Claudius Ptolemy’s work
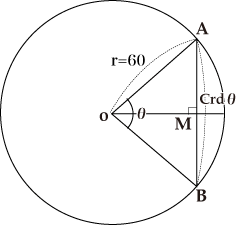
2§5 We can see how these functions operate in the first table of Ptolemy’s Almagest. After a prefatory address (Almagest 1.1), Ptolemy defines in sections 1.2-1.9 a systematic outline of his work, organized so that, in the tradition of Greek mathematics, each successive point can be established through formal proof. Before Ptolemy can even address the first topic, however, he needs to establish the single trigonometric function used in ancient Greek astronomy, the chord. The chord is a straight line between two points on a circle. In Figure 1, the chord of angle θ is line segment AB.[2]
2§6 In Almagest 1.10, Ptolemy demonstrates a convenient method for calculating this value for an angle of any given size, and then provides the results in a table (Almagest 1.11).
2§7 Figure 2 illustrates this table in the oldest extant manuscript of the Almagest, now in Paris.[4] An entire page is devoted to a table (here called a κανόνιον) separated into two sections of 45 lines each.[5] In the left panel, the leftmost column labelled “arcs” (περιφερειῶν) gives successive angles in units of 1/2 degree, from 1/2 to 22 1/2 degrees. The adjacent three columns, labelled “straight lines” (εὐθειῶν), give the length of the chord; these are followed by four columns giving an average value to use in interpolating between half-degree angles.[6] The same pattern is repeated in the right panel with values for angles from 23 to 45 degrees.

2§8 Through the first nine sections of the Almagest, the reader has presumably followed Ptolemy’s rigorously ordered logic sequentially, but section 1.10 explains why and how we must apply a different kind of reading to the table seen on folio 17. The preceding sections define a reliable method for recomputing values if there is suspicion of a scribal error, but the explicit expectation is that the working scholar will treat the table as a function. Begin with a value in its domain: an angle from 0 to 45 degrees. Read down the left-most column until you find the nearest half degree to your angle, then read across that row to find the length of the chord for that half degree. If your angle is not an exact half degree, then read further across the row to find the appropriate value to use in interpolating your exact angle.
2§9 The pattern of extensive formal proofs followed by summary table is repeated throughout the Almagest. Each major section of the work concludes with a table summarizing the results of that section; taken together, they effectively outline the entire program of the Almagest.[7] Ptolemy’s explicit comments also highlight the importance of tables in fulfilling his goal of creating a practical resource for working scientists. After demonstrating the method for deriving values for a new table, he regularly explains the organization and use of the resulting table, and repeatedly emphasizes how the table will provide a more useful form for a working scientist. Ptolemy makes clear that the text of the Almagest is not to be read as an uninterrupted linear flow, but leads to functional utilities that scientists will return to repeatedly. A particularly clear example occurs in 6.12, where even the utility of a table is trumped by a specially designed diagram that Ptolemy prefers “for its ease of visual use” (κατὰ τὸ εὐθεώρητον).
2§10 No other ancient author exults in tables like Claudius Ptolemy. Whether he is writing about astronomy, geography[8], musical harmony, optics or even the epistemological basis of science[9], he creates tabular structures that his readers can consult for convenient reference. He even, uniquely, chooses to make an individual, public dedication in the form of a table. The stele he dedicated to “the Savior God” at Canobus has not survived, but its text has been preserved in a handful of manuscripts. Ptolemy listed in tabular form a series of crucial cosmological constants that he had discovered or verified.[10] The contrast with Archimedes, whose funerary marker famously displayed a geometric feature summarizing his greatest discovery, is irresistible.[11]
2§11 Ptolemy even creates a work that adopts the plural term “tables” for its title. The Handy Tables (πρόχειροι κανόνες) bring together a series of tables in a single volume or codex. If a single κανών in the Almagest embeds a function resembling a single “app” accompanying the explanatory text, then the κανόνες are a collection of apps together resembling a “device”. They are handy in all senses of that term: practical, with no linear text to distract from the very different manner consultation used for these tabular structures, with all the functions you need for astronomy in a single device, but also, literally, palm sized. The manuscripts of the Handy Tables seem to favor unusually compact dimensions: one of the oldest, Bibliothecae Publicae Codex Graecus 78 in the Leiden University Library, measures 190mm x 145 mm; for comparison, Apple’s tech specs list the dimensions of the iPad mini as 200mm x 135mm.
2§12 It is significant that the Handy Tables include chronological tables that are not found in the Almagest, but without which the chronological computations of the Almagest are impossible.[12]

2§13 The Handy Tables, like the use of tables throughout Ptolemy’s extant corpus, underscore that the mathematicians’ generic definition of functions as mappings from domain to range is in no way restricted to purely mathematical data in our sense. The geographically organized selection of “important cities” (πόλεις ἐπίσημοι) relates instead to the Geography

2§14 Two other works with “tables,” plural, in their title show that scholars in diverse disciplines could assemble collections of “apps” for different purposes.
Eusebius, Chronological Tables
2§15 Ptolemy’s chronological tables serve a narrowly astronomical purpose. They allow the astronomer to construct an unbroken day count from the time of Nabonassar onward, in a manner similar to Scaliger’s reconstruction of a Julian era, or to modern astronomers’ use of a Julian day count. They were intended to reconcile diverse historical records in competing calendars and eras.
2§16 Eusebius’ Chronological Tables (χρονικοὶ κανόνες) no longer survive in Greek, but we can get an idea of their organization from the extant versions of the text in Armenian and in the rich history of its Latin version by Jerome. Eusebius’ aim was to coordinate the chronology of contemporary regnal sequences in different parts of the world at different times, and to place historical events in the appropriate place in these synchronisms. Rows of his table represent individual years; columns either list historical events, or give a running count in one of the aligned regnal sequences. Different tables are necessary as the historical ebb and flow of kingdoms demands more or fewer columns of regnal sequences to align. Eusebius unites Christian and pagan historical records in a single, long arc. Visually, the vast sweep of history narrows the columns of historical powers until Rome alone remains. With Eusebius, this teleological funneling would have then culminated in the lifetime of his patron and subject of his biography, Constantine.
2§17 In his Latin preface to his translation, Jerome gives an invaluable glimpse of how this genre was understood. In addition to taking on the difficult task of rendering Eusebius in Latin, he has expanded the content in two ways. He has, most obviously, extended the chronological coverage beyond the time of Eusebius to Jerome’s day, but he has also, he tells us, added content of interest to his western, Latin audience, for the period from the fall of Troy to the end of Eusebius’ work.
2§18 At the same time, Jerome insists that scribes should meticulously follow the color scheme he uses to distinguish visually the structure of the tables. Jerome is a fascinating witness that scholars of chronology could insist on structural integrity while expecting content to be modified.
2§19 Jerome’s injunction to replicate his color scheme is not observed in the manuscripts, but his expectation that later scholars would treat his tables as he treated those of Eusebius is well attested. In this kind of genre, it is a mistake to expect that we can follow traditional critical methods to reconstruct an archetype. Instead, what the manuscripts show is a living, and constantly updated tradition.[13]
Theodosius of Alexandria, Introductory Tables of Noun Declensions and Introductory Tables of Verb Conjugations
2§20 In the study of language, even introductory material could be organized in functional tables, as the grammarian Theodosius of Alexandria does in two works entitled Introductory Tables, one devoted to noun declensions, one to verbal conjugations.
2§21 Although the title of the texts again explicitly claims the plural “Tables”, and individual sections of the text are labelled “Table”, the tabular structure essentially vanishes in the standard print edition.[14] In Figure 5, we see table 1 in the Tables of Noun Declensions, giving us the declension of the noun Ἄιας. There is no indication of rows or columns. Where are we to find the “key”, and where is the “value” of the table?

2§22 If, however, we turn to the manuscripts, we see that the scribes unambiguously distinguish the domain and range of the function, as folio 3 recto of the Leiden manuscript Voss 76 illustrates (figure 6). A rule is given in a normal, cursive script. The beginning is clearly set off by the large outlined capital letter. The output applying the rule is then set off by clear space, written in a distinct semi-uncial script, and highlighted with a color overlay.

2§23 All of these texts collect a series of tables that, together, create a kind of domain-specific “device” for open-ended consultation and retrieval of data. As different as the texts are in their contents, the manuscripts emphasize the tabular structures with various forms of visual highlighting. This is often lost in modern print editions, where tables turn into an undifferentiated sea of black ink on white pages.
Shared scholarly practices
2§24 In each of the example texts cited here, the use of tabular structures merits a far fuller analysis than is possible in this forum, but I hope that collectively these illustrations argue for a reconsideration of sharply drawn distinctions between “literary” and “scientific” scholarship. Classicists have not hesitated to assert these categorizations as givens[15], but the difference immediately founders on any attempt to recognize disciplines by textual genres.[16]
2§25 Because the written text was the preeminent medium of organizing and disseminating scholarly information in all fields, all scholars in antiquity were in fact textual scholars to a greater or lesser degree. It is remarkable that in the systematic preface to the Almagest, Ptolemy describes his writing with the verb ὑπομνηματίζω, and echoes this language in the epilog. Even though his text is concerned with the permanently observable realities of the physical world, Ptolemy thinks of his research as adding to scientific knowledge by creating a commentary on the work of his predecessors.[17] (We should also remind ourselves that the only commentary extant from the Hellenistic period is by the era’s greatest astronomer, Hipparchus, and comments not only on the mathematically oriented Phaenomena of Eudoxus, but also on the didactic poem of the same name by Aratus.)[18] The fact that scholars from grammarians to astronomers used tables to express essential parts of their writing should not therefore surprise us. They worked in the same technical infrastructure, and applied widely known techniques much as scholars in diverse disciplines today might adopt common techniques for organizing databases, or apply common methods to similar kinds of statistical analyses.
2. Functional editions today
3§1 Whatever our views on cross-disciplinary connections among ancient Greek scholars, their regular reliance on functional texts challenges us to ask how we should conceive of functional editions of their work in 2016. The processes required to produce texts on papyrus scrolls, parchment codices or mass-printed books with paper pages certainly differ, but until the late twentieth century the defining characteristic of all written texts was that they encode their symbols on physical artifacts. Scholars of my generation grew up and were trained in this world. Scissors were part of my writing equipment when I was a graduate student: “cut and paste” had not yet become a metaphor.
3§2 That is no longer true, and neither my generation nor our children have fully come to terms with what it means to edit a text digitally. We are living through, but have not yet fully comprehended, a transformation as dramatic as that of writing. While writing defines a system of symbols to represent the system of symbols in spoken language, digital information defines a system of digital symbols to represent writing’s system of symbols, in turn representing the symbols of spoken language. Writing created texts freed from speech’s limitations of time and space: digital technology creates texts further freed from fixed, physical form.
3§3 Unlike the editor of a written text, who relies on visual cues to imply meaning, the editor of a digital text must explicitly describe its semantic structure rather than its appearance. An epigraphist or papyrologist working in print media might insist on the importance of underdots to imply an uncertain reading: the digital editor instead must refer explicitly to uncertainty. In a visual presentation, uncertainty might be represented by underdots, or perhaps instead by a difference in color (say, grayed out text). Computer screen readers might vocalize a comment. Different analyses of the text’s content might choose to ignore or include content with uncertain readings.[19]
3§4 In the previously presented examples of manuscripts with tables, medieval scribes used a variety of visual cues to highlight the fact that tables were to be distinguished from linear text: position on the page, of course, and often titles, but also color, distinct form of script, and decorative patterns pointing out the table or units in the table. They understood that simply reproducing the table’s text was not an adequate representation of its distinct function. Some print editions have also in some way recognized the distinct status of the table. An extreme approach is to omit them. The most recent Engish and French translations of Ptolemy’s Geography both choose to handle only the “theoretical” sections of the text, and present samples of a table so that readers can get some idea of what they are like.[20]
3§5 What is the semantic structure of a functional table in an ancient Greek scholarly work? When tables serve as functions, in the mathematical sense, how should we represent that section of a text alongside more familiar, linear prose? Our aim as editors should not, in the first place, be to reproduce the visual form of a table, but instead to represent the semantics of a function. Just as a semantically encoded linear text in a digital edition might be visualized or manipulated in any number of ways (underdots vs color highlighting), functions can assume different forms. The example of Ptolemy’s Table of Chords suggests one obvious possibility. In high school trigonometry class, I learned to use similar tables in our text book to look up the sine of an angle; today that function is familiar as an app on a computer or phone.
3§6 The tables in Ptolemy’s Geography are a function for looking up sites in a geographic database. A digital edition of the Geography should recognize that, and enable working with the tables as a geographic database — something that a geography app could use. We might want to create a reading interface that queries the properties recorded in Ptolemy’s carefully organized tables: political province, type of site, physical geographic region, cultural or ethnic association. Or we might want an interface that eschews a textual presentation altogether, and instead renders the data as Ptolemy himself intended, in the form of geographic maps.
3§7 While the data set in Ptolemy’s Geography records unique data, Theodosius’ grammatical tables are meant to be paradigms. They serve as a test case for a more general function: if you can conjugate τύπτω, then you should also be able to conjugate λύω. This is content for a “grammar testing app.” We cannot list every possible Greek verb, so representative data must stand in for the entire domain. This corresponds closely to what software developers would call unit tests, specific test instances of a more general function. A semantic edition of Theodosius should recognize this, and enable working with his tables as instances to test with a Greek morphological parser.
3§8 In the software package accompanying this article (as explained below), I include digital editions of Ptolemy’s Geography and of Theodosius’ Introductory Tables. Both editions organize the tables embedded in the text for use by apps, and each edition is complemented by one example of an app implementing a non-linear reading of the text that would not be possible with analog media. For Ptolemy’s Geography, a textual view and a cartographic view interact. A map viewed in Google Earth includes links to a text service retrieving the corresponding passage of text; traditional textual views include search keys for finding locations on the cartographic view. Theodosius’ paradigms are treated as unit tests. Rows in the table are viewed as assertions such as “The second singular present indicative active of τύπτω is τύπτεις.” Theodosius’ table maps the identification of a form such as “second singular present indicative active of τύπτω” to a value such as τύπτεις. In unit testing, this is called the “expected value.” In our testing app, the identification of the form is submitted to an automated morphological parser. The result is called the “actual value.” If the actual value agrees with the expected value, then the test passes, and the form is highlighted in green in the text of the table. If the actual value and the expected value do not agree, the test fails, and the form is highlighted in the text in red. In software development as in grammatical drilling of beginning Greek students, the assumption is that the expected value is authoritative, so when the test fails, the system being tested (automated parser or beginning Greek student) has erred.
3§9 The digital editor cannot hide from the fact that editing a text is a complex interpretive act. As digital editions enable new forms of “reading,” we may come to understand ancient texts differently, and recognize a need for new, not yet realized forms of editions. I have argued for a view of tables as functions in Greek scholarship in part for the simple reason that readily available digital photography of manuscripts has allowed me to view and compare manuscripts of scholarly texts. That would have been impossible a decade ago. Understanding tables as functions suggests a new approach to editing, and leads to the new forms of digital editions included in this article’s accompanying software. Perhaps these or other digital editions will suggest a perspective on our texts that will in turn require a new kind of edition.
3§10 Editing, as an interpretive act, is an inherently iterative practice that evolves in the same ways that the practice of reading evolves. Working digitally underscores the fact that editions are not static, permanently fixed ideals, but the expression of an evolving understanding of a text.
3§11 At the same time, editions aim more directly at reuse by other scholars than many other forms of scholarly production. Digital editors are as motivated as any to ensure that their work is not tied to specific, ephemeral technologies. The challenges of creating a digital edition typify the challenges facing scholars more generally as they try to understand what it means to work with digital technologies in 2016. This article has presented both a reading of a group of ancient texts, and a response to that reading trying to reimagine how digital editions could capture some of the practical, open-ended used desired by ancient scholars.
3. A functional continuation of the discussion
4§1 One of the most jarring hold overs from pre-digital practices is a regular feature of articles about digital scholarship. Scholars use computers to develop some digital resource; they then use the same computers to compose articles about what they have done; yet the digitally created articles and their digital subjects remain unconnected. Clearly, we have not yet achieved a digital integration of prose discussion and interactive functionality comparable to the interweaving of expository prose and functional tables in the texts of ancient Greek scholars. We may console ourselves with the thought that Hellenistic and Roman scholars worked in a highly literate world with centuries of experience of writing before they began to apply tabular structures to the needs of scholarship, while we are still in the early decades of work with digital information structures that sometimes seem to change form more rapidly than Proteus wrestling Menelaus.
4§2 But it is not too early to attempt some degree of digital integration, especially since, in order to gain experience with the possibilities of digital technology, we will need to adopt from digital developers the unfamiliar attitude of “fail fast, fail often.” While the digital text of this article will not interact directly with experiments in digital editing, I am taking advantage of the Center for Hellenic Studies’ openness to new forms of publication to include alongside it software offering interactive access to digital editions of some of the texts discussed here.[21]
4§3 In the sometimes heated current debate about what digital technologies mean for the creation and use of texts, my goals are modest. Like Claudius Ptolemy, my aim is to offer a practical contribution.[22] Like Hipparchus, I hope that it may be a service to others.[23]
Appendix: table of tables in the Almagest
| Passage | Table |
| 1.11 | Table of chords |
| 1.15 | Table of inclination |
| 2.8 | Table of rising times at 10-degree intervals |
| 2.13 | Table of zenith distances and ecliptic angles |
| 3.2 | The sun’s mean motion |
| 3.6 | The sun’s anomaly |
| 4.4 | Mean motion of the moon |
| 4.10 | Simple lunar anomaly |
| 5.8 | Complete lunar anomaly |
| 5.18 | Parallax for sun and moon |
| 6.3 | Conjunction and opposition of sun and moon |
| 6.8 | Eclipses |
| 6.12 | Angles of inclination at eclipses with the horizon |
| 7.5 | Constellations in northern hemisphere |
| 8.1 | Constellations in southern hemisphere |
| 9.4 | Mean motions in longitude and anomaly of the five planets |
| 11.1 | Position in longitude of the five planets |
| 12.8 | Stations |
| 12.10 | Greatest elongations of Venus and Mercury with respect to sun |
| 13.5 | Planetary latitude tables |
| 13.10 | First and last visibilities |
Sources cited
Asper, M. 2007. Griechische Wissenschaftstexte. Stuttgart.
Aujac, G. 1993. Claude Ptolémée, astronome, astrologue, géographe : Connaissance et représentation du monde habité. Paris.
Berggren, J.L., and B.R. Goldstein. 1987. From ancient omens to statistical mechanics: essays on the exact sciences presented to Asger Aaboe. Copenhagen: University Library, 1987.
Berggren, J.L., and A. Jones. 2002. Ptolemy’s Geography: An Annotated Translation of the Theoretical Chapters. Princeton.
Danielewicz, P. 2005. “Further Hellenistic Acrostics: Aratus and Others.” Mnemosyne 58.3: 321-334.
Dickey, E. 2007. Ancient Greek Scholarship. Oxford.
Hamilton, N.T., N.M. Swerdlow, and G.J. Toomer. 1987 “The Canobic Inscription: Ptolemy’s Earliest Work.” In Berggren and Goldstein 1987:55-73.
Hanley, C., S. Merola, and S. Neville. 2016. “Tracing the Scribal Tradition with Diplomatic Editions of Manuscripts of Jerome’s Chronicle.” New England Classical Journal 43.2:77-94.
Hopkinson, N. 2015. Theocritus, Moschus, Bion. Loeb Classical Library 28. Cambridge and London.
Huby, G., and G. Neal, ed. 1989. The Criterion of Truth. Liverpool.
Jaeger, M. 2008. Archimedes and the Roman imagination. Ann Arbor.
Lewis, N. 1974. Papyrus in Classical Antiquity. Oxford.
Matthaios, S., F. Montanari, and A. Rengakos. 2011. Ancient Scholarship and Grammar. = (Trends in Classics: Supplementary Volumes, 8). De Gruyter.
Pedersen, O. 1974. A Survey of the Almagest. Odense University Press. == Acta Historica Scientiarum Naturalium et Medicinalium 30.
Pfeiffer, R. 1968. History of Classical Scholarship. Oxford.
Ramsay, S. 2011. Reading Machines: Toward an Algorithmic Criticism. University of Illinois.
Sharples, R.W. 1989. “Appendix on the table.” In Huby and Neal 1989:227-230.
Toomer, G.J. 1984. Ptolemy’s Almagest. Duckworth.
[1] Recent discussion of Hellenistic acrostics including review of previous work: Danielewicz 2005. We even find acrostics in pattern poems: Hopkinson 2015 562-563, with bibliography on Besantinus (or perhaps Bestinus).
[2] As this illustration implies, there is a direct relation of the chord to the trigonometric sine. Use your knowledge of Euclid book 1 to bisect angle θ, and at point M you will also bisect AB, the chord of θ. Since AM and MB are each equal to the sine of the bisected angle, we have a general relation: the chord of θ is equal to two times the sine of one-half of θ, or, crd(θ)=2sin(θ/2).
[3] Illustration reproduced from http://www.ndl.go.jp/math/e/s1/c8.html.
[4] Paris, Bibliothèque Nationale, ms. grec 2389. Non-commercial reuse of image from Gallica pursuant to terms of French law n°78-753 of July 17, 1978. http://gallica.bnf.fr/ark:/12148/btv1b8470171d/f41.item.r=grec%202389
[5] Toomer notes that 45 lines is the standard height of tables throughout the Almagest and presumably corresponds to a standard height papyrus roll: Toomer 1984, 56. Translation and commentary on the locus classicus in Pliny NH 13.78: Lewis 1974, 36-39, 56.
[6] The chord length is measured in sixtieths of the radius (called “parts”). The right-most four columns give the average average increment in length for each minute of arc (“sixtieths”). For a detailed discussion of Ptolemy’s chord table: Pedersen 1974, 56-65.
[7] See Appendix 1 for a complete list of the tables in the Almagest.
[8] In the Geography, the data base of more than 6,000 sites identified with longitude and latitude values is the largest scientific data set to come down to use from antiquity. The second largest is the star catalog in books 7-8 of the Almagest.
[9] Sharples 1989.
[10] Published by Heiberg in the Teubner edition of Ptolemy, vol. II, Opera Astronoomica Minora.
[11] On the geometric figure of Archimedes’ tomb as a rhetorical device for Cicero: Jaeger 2008, 32-47.
[12] On Ptolemy’s chronological methods in the Almagest, Toomer 1984: 9-14.
[13] Jerome’s Chronicles as a living, constantly updated genre: Hanley et al. 2016.
[14] Theodosii Alexandrini Canones, Teubner edition of A. Hilgard, 1889 = vol. 4.1 in the Teubner series of Grammatici Graeci.
[15] Pfeiffer opens his essential work on classical scholarship with the statement “Scholarship is the art of understanding, explaining, and restoring the literary tradition” (Pfeiffer 1968: 3). For a recent example of an equally axiomatic statement, the editors of Matthaios et al. 2011 open the introduction to their volume by equating “ancient Greek scholarship” with γραμματικὴ τέχνη. Asper 2007 offers an important challenge to these assertions.
[16] Although the full title of Dickey 2007 Ancient Greek Scholarship: A Guide to Finding, Reading, and Understanding Scholia, Commentaries, Lexica, and Grammatiacl Treatises and explicit comments might suggest that she shares Pfeiffer’s assumptions, in fact her persistence in maintainting her announced focus on scholarly genres of text leads her to discuss Aratus and Euclid in successive sections, and Apollonius of Perga immediately after Apollonius of Rhodes. Her valuable introduction to reading scholarly Greek clearly shows that the similarities of commentaries and scholia as scholarly genres extend to numerous specific habits of speech and thought.
[17] Almagest 1.1 describes Ptolemy’s work as starting from what others have established (μανθάνοντες τὰ ἤδη κατειλημμένα), then adding his own commentary to it (πειρασόμεθ α ὑπομνηματίσασθαι). The metaphor throughout is textual. The epilog (Almagest 13.11) refers to the text as a ὑπομνηματισμός. ὑπόμνημα would be more familiar in the sense “commentary”; with ὑπομνηματισμός, Ptolemy emphasizes the modest, pratical aim of his work, but the echo of the proem is unmistakable. Eustathius uses ὑπομνηματισμός in the sense of “commentary”: LSJ, ὑπομνηματισμός.
[18] Hipparchus’ comments comparing the persuasiveness of poetic χάρις with the more “scientific” or “demonstrative” logic of Eudoxus deserve extended study in their own right.
[19] Stephen Ramsay argues that critical procedures involved in reading physical texts (including “translating” a passage into the language of the reader, and drawing up lists of readings) have direct analogies with the activities of digital editors, and borrows McGann and Samuels’ term “deformance” to describe the process. Ramsay 2011.
[20] Berggren and Jones 2002; Aujac 1993.
[21] For information about the semantically structured digital editions and software for “reading” or working with them functionally, see http://appsinvellum.github.io/.
[22] Ptolemy even chooses end the Almagest with an epilog returning to repeated theme of “utility” vs. “accusation” (ἔνδειξις) (Almagest 13.11).
[23] Hipparchus, Commentary, 1.1.6.
