The Reception of the Distance-Period Relationship in the Capellan and Copernican Cosmologies

Pre-doctoral Fellow in Hellenic Studies 2022–23

From ancient times until the early modern period, determining the arrangement of the planets (forma mundi) posed one of the most difficult and urgent inquiries in the field of cosmology. In his cosmological system, Plato did not resolve the forma mundi problem; rather, he left it as an area for further research. Although Plato did not solve the forma mundiproblem, he did establish one of the most significant astronomical principles in the history of astronomy, namely the distance-period relationship (i.e., the planets with larger orbits have more extended periods of revolution),¹ which can be found in the Aristotelian corpus as well.² By adopting that principle, Nicolaus Copernicus was able to unveil the true structure of our solar system. Even though a multitude of studies concerning the history of astronomy is availablethere is still a broad consensus among modern scholars that Copernicus’ heliostatic cosmology was the first consistent application of the above-mentioned principle.³ But, as I argued in my paper “The Impact of the Platonic Distance-Period Relationship on Martianus Capella’s Astronomy”, available in the First Drafts@Classics@ of the CHS, Martianus Capella’s geoheliocentric system consistently implemented a basic form of the distance-period relationship for the order of the planets by grouping those celestial bodies that did not conform with the distance-period relationship in order to solve the forma mundi problem, just like Copernicus eleven centuries later.

Which was one crucial factor preventing a purely geocentric cosmological model from resolving the issue of the arrangement of planets? The orbits of the inner planets being enclosed by the Earth’s, produce the apparent phenomenon according to which Mercury and Venus complete the ecliptic in a solar year (on average). If one adheres to the distance-period relationship, it would suggest that these celestial bodies are equidistant from Earth, which would have been considered quite problematic for both astronomical and physical reasons. Subsequently, there was no consensus among astronomers/natural philosophers regarding the exact positions of the aforementioned celestial bodies. Capella inherited the longstanding forma mundi problem, which had persisted throughout the ages, and cut the Gordian knot adopting circumsolar orbits for the inner planets, therefore grouping Mercury and Venus in a common system with the Sun at its center.⁴

Capella applied the astronomical principle formulated by Plato, treating the Sun, Mercury, and Venus, as a common system, due to their periods of revolution. Bruce Eastwood made a remarkable discovery when he found an 11th-century manuscript of the Timaeus that included Capellan diagrams –diagrams depicting circumsolar orbits for Mercury and Venus– inserted into 39a, where Plato had originally formulated the distance-period relationship.⁵ Capella remained faithful to the distance-period relationship and arranged the planets outside of the Sun-Mercury-Venus system in the following order: Mars, which completes its orbit in 2 years, followed by Jupiter in 12 years, and finally Saturn in 30 years. As a result, Capella decided to use a geoheliocentric model that would maintain the distance-period relationship. He utilized an imprecise version of Kepler’s harmonic law, which was discovered many centuries later, to ascertain the planetary positions, i.e.:

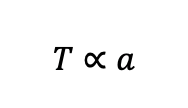
where is T the orbital period and a is the distance from Earth.

Capella calculated the lunar orbit around the Earth as 100 times greater than the Earth’s circumference (for the Earth’s circumference Capella offered two different values: in VIII. § 858 of De nuptiis Philologiae et Mercurii Capella adopted the value of 406,010 stadia, although, in § 596, he gave the correct value of Eratosthenes’ estimation, i.e., 252,000 stadia).⁶ According to Capella, the distances of the rest of the celestial bodies are multiples of the lunar orbit in conformity with their periods. Given the formula

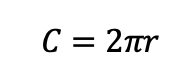
where C represents the circumference of a circle and r denotes its radius, we can calculate the radius of a particular planet’s orbit using the following equation:

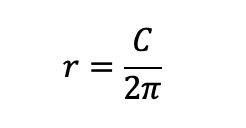
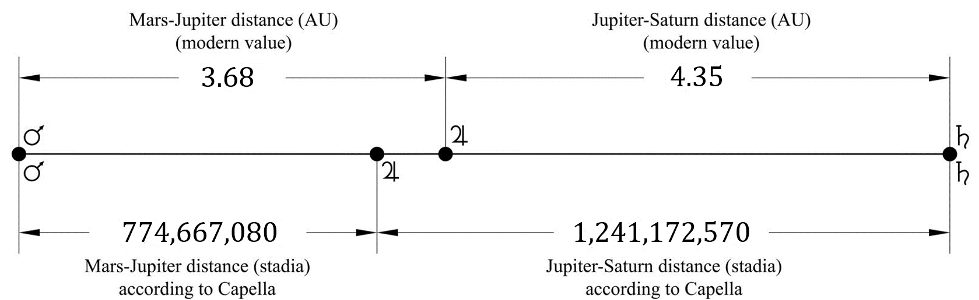
Assuming that the lunar orbit equals 1, then the Earth-Moon axis equals (r = 1/2π).⁷ Capella’s reasoning suggests that the orbit of the Sun-Mercury-Venus system is believed to be 12 times larger than the orbit of the Moon. This conclusion is based on the observation that these celestial bodies complete one full orbit around the ecliptic within a year consisting of 12 months. Therefore, the Sun-Mercury-Venus system lies 1.91 times farther from Earth (r = 12/2π); similarly, Mars’ orbit lies 3.82 times farther from Earth (r = 24/2π) with 24 months period or 2 years; Jupiter 22.9 (r = 144/2π) with 144 months period, and Saturn 53.47 (r = 336/2π) with 336 months period.⁸ Consequently, if we place those values into a logarithmic scale [Chart 1], we get a straight line because the distance from Earth (in log₁₀(stadia)) grows linearly per unit of time (in log₁₀(months)).

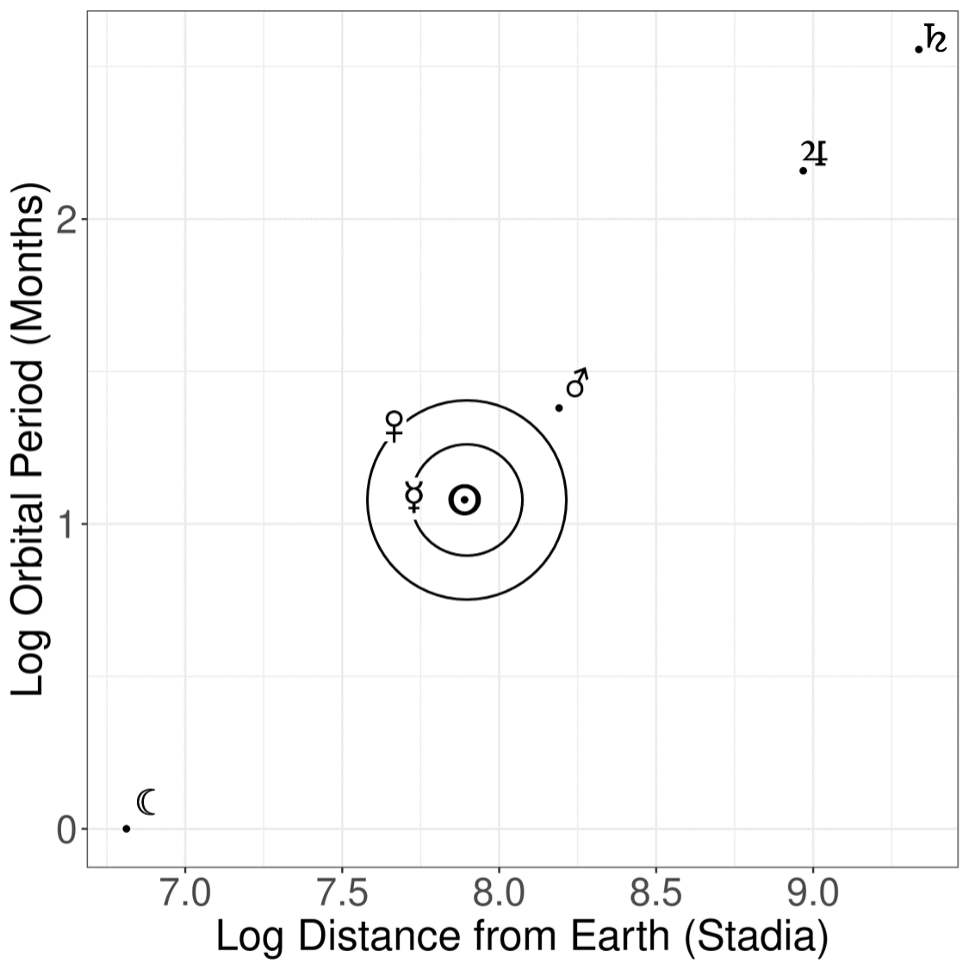
Interestingly enough, by comparing the Capellan values for the distances of the outer planets with the modern ones, we can see that Capella’s adoption of the distance-period relationship (in the form of T ∝ a) led him to a fair approximation of the relative positions of Mars, Jupiter, and Saturn [Figure 1].

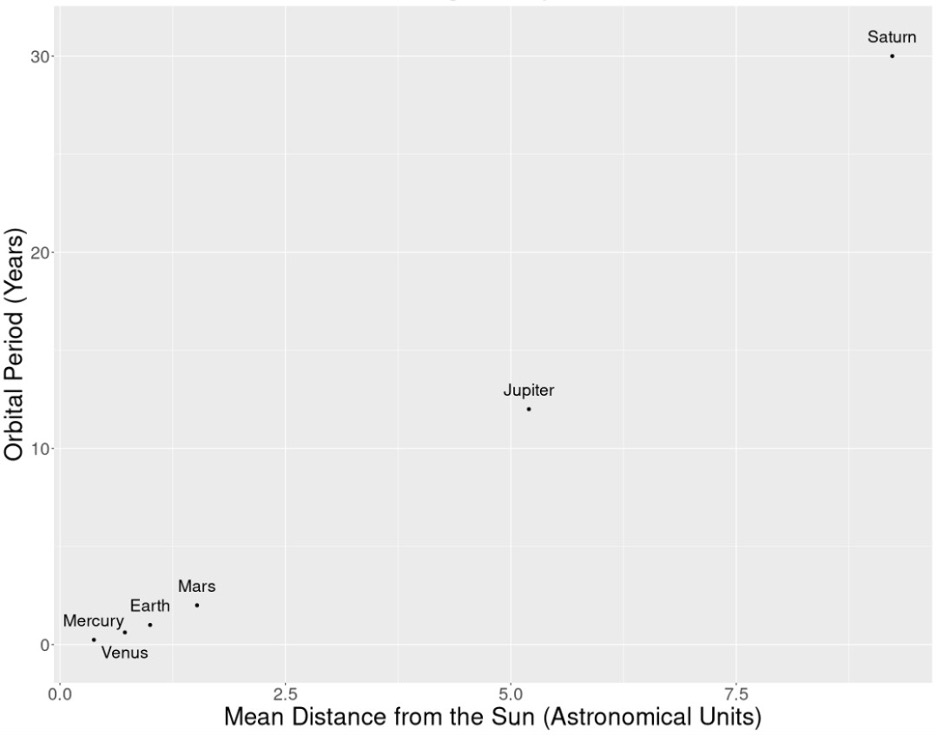
Nicolaus Copernicus’ development of the heliostatic model of the universe, in which the earth was postulated to orbit the stationary mean Sun, is widely recognized as a seminal contribution to the Scientific Revolution. This revolutionary theory has cemented Copernicus’ place as one of the most important astronomers in history, and his work paved the way for further advancements in astronomy and related fields. The development of Copernicus’ model enabled the creation of a comprehensive model of the solar system, with the size of the Earth’s orbital radius serving as the scale for the entire known system. The Copernican model follows a different version of the distance-period relationship that corresponds to what is now known as the third law of planetary motion (T² ∝ a³), even though Copernicus himself was not aware of this law at the time. Both Copernicus and Capella assumed constant speeds for the planets and placed them based on their periods of revolution. In his well-known “U” notes, Copernicus used trigonometry to compute the relative distances of the inner and outer planets during maximum elongation and quadrature, respectively.⁹ This allowed him to determine the precise order of the cosmos. Indeed, there is a clear correlation between the mean planetary distances calculated by Copernicus and the periods of the planets [See table below and chart 2].

Planet	Copernicus’ “U” notes in AU (fol. 15v)	Modern Value in AU	Orbital Periods of the Planets(De Revolutionibus, fol. 9b)
Mercury (☿)	0.3696	0.387	80 days
Venus (♀)	0.72	0.72	9 months
Earth (⊕)	1	1	1 year
Mars (♂)	1.52	1.52	2 years
Jupiter (♃)	5.2	5.2	12 years
Saturn (♄)	9.2	9.54	30 years

In a manner akin to Capella, Copernicus also placed his trust in the distance-period relationship and regarded it as an essential factor in resolving the problem of the order of the planets. Both astronomers had, among others, Plato as their mentor and attempted to establish a unified astronomical system. Although Capella had already consistently applied a basic form of the Platonic distance-period relationship before him, Copernicus was the one who geometrically applied it in a “non-arbitrary” way and indisputably discovered the actual framework of the cosmos that fulfilled Plato’s aspiration.

Acknowledgments

The research work was supported by both the Center for Hellenic Studies (Harvard University) and the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the 3rd call for H.F.R.I. Ph.D. Fellowships (Fellowship Number: 5160).

Bibliography

Athanasakis, A. “The Impact of the Platonic Distance-Period Relationship on Martianus Capella’s Astronomy.” First Drafts@Classics@, CHS, Harvard University (2023).

Athanasakis, A. “The Copernican System and the Celestial Spheres.” Φιλοσοφία 51. Yearbook of the Research Centre for Greek Philosophy at the Academy of Athens (2021): 241-259 [in Greek].

Athanasakis, A. “Copernicus, Nicolaus.” In Encyclopedia of Renaissance Philosophy, edited by Marco Sgarbi. Cham: Springer, 2021.

Berry, A. A Short History of Astronomy, from Earliest Times through the Nineteenth Century. New York: Dover Publications, 1898.

Bulmer-Thomas, I. “Plato’s Astronomy.” The Classical Quarterly 34, no. 1 (1984): 107-12.

Burnyeat, M. “Plato on Why Mathematics is Good for the Soul.” In Mathematics and Necessity: Essays in the History of Philosophy, edited by T. Smiley, 56-81. Oxford: Oxford University Press, 2001.

Copernicus, N. On the Revolutions. Translated by Edward Rosen. Baltimore: The Johns Hopkins University Press, 1992. Originally published as volume 2 of Nicholas Copernicus: Complete works. Warsaw: Polish Scientific Publishers, 1978.

Cornford, F. M. Plato’s Cosmology: The Timaeus of Plato. Indianapolis: Hackett Publishing Company, Inc, 1937.

Dicks, D. R. Early Greek Astronomy to Aristotle. New York: Cornell University Press, 1985.

Dreyer, J. L. E. A History of Astronomy from Thales to Kepler. New York: Dover Publications, 1953.

Eastwood, B. S. “Plato and Circumsolar Planetary Motion in the Middle Ages.” Archives d’Histoire Doctrinale et Littéraire du Moyen Âge 60 (1993): 7-26.

Eastwood, B. S. Ordering the Heavens: Roman Astronomy and Cosmology in the Carolingian Renaissance. History of Science and Medicine Library, 4. Medieval and Early Modern Science, 8. Leiden: Brill, 2007.

Gingerich, O. God’s Planet. Cambridge, MA/London, UK: Harvard University Press, 2014.

Goddu, A. “Reflections on the Origin of Copernicus’s Cosmology.” Journal for the History of Astronomy 37, no. 1 (2006): 37-53.

Goldstein, B. R. “Copernicus and the Origin of his Heliocentric System.” Journal for the History of Astronomy 33, no. 3 (2002): 219-235.

Goldstein, B. R. “The Arabic Version of Ptolemy’s Planetary Hypotheses.” Transactions of the American Philosophical Society57, no. 4 (1967).

Gregory, A. Plato’s Philosophy of Science. London: Bristol Classical Press, 2001.

Koyré, A. The Astronomical Revolution: Copernicus, Kepler, Borelli. Translated by R.E.W. Maddison. Ithaca: Cornell University Press, 1973.

Kuhn, T. The Copernican Revolution. Cambridge, MA: Harvard University Press, 1957.

Martianus C. De nuptiis Philologiae et Mercurii. Edited by James Willis. Leipzig: B.G. Teubner Verlagsgesellschaft, 1983.

Mourelatos, A. P. D. “Plato’s «Real Astronomy»: Republic 527d-531d.” In Science and the Sciences in Plato, edited by J. P. Anton, 107-120. New York: Caravan Books, 1980.

Neugebauer, O. A History of Ancient Mathematical Astronomy. 3 vols. Berlin: Springer, 1975.

Omodeo, P. D. Copernicus in the Cultural Debates of the Renaissance: Reception, Legacy, Transformation. Leiden: Brill, 2014.

Ptolemy. Claudii Ptolemaei Opera Quae Exstant Omnia, Syntaxis Mathematica. Edited by J. L. Heiberg. Leipzig: vols. 1.1 and 1.2, 1898-1903.

Siraisi, N. G. Medieval and Early Renaissance Medicine: An Introduction to Knowledge and Practice. Chicago: University of Chicago Press, 1990.

Stahl, W., R. Johnson, and E. Burge. Martianus Capella and the Seven Liberal Arts. New York & London: Columbia University Press, 1971.

Stahl, W. “To a Better Understanding of Martianus Capella.” Speculum 40, no. 1 (1965): 102-115.

Swerdlow, N. M. “Copernicus, Nicolaus (1473-1543).” In Encyclopedia of the Scientific Revolution, edited by Wilbur Applebaum, 162-168. New York: Garland Publishing, 2000.

Swerdlow, N. M., and Otto Neugebauer. Mathematical Astronomy in Copernicus’s De Revolutionibus. 2 vols. New York: Springer, 1984.

Vesel, M. Copernicus: Platonist Astronomer-Philosopher, Cosmic Order, the Movement of the Earth, and the Scientific Revolution. Bern: Peter Lang, 2014.

Vlastos, G. Plato’s Universe. Las Vegas: Parmenides Publishing, 2006.Westman, R. 1980. “The Astronomer’s Role in the Sixteenth Century: A Preliminary Study.” History of Science 18, no. 2 (1980): 105-147.

---

¹ See Timaeus 38e-39a: Ἐπειδὴ δὲ οὖν εἰς τὴν ἑαυτῷ πρέπουσαν ἕκαστον ἀφίκετο φορὰν τῶν ὅσα ἔδει συναπεργάζεσθαι χρόνον, δεσμοῖς τε ἐμψύχοις σώματα δεθέντα ζῷα ἐγεννήθη τό τε προσταχθὲν ἔμαθεν, κατὰ δὴ τὴν θατέρου φορὰν πλαγίαν οὖσαν, διὰ τῆς ταὐτοῦ φορᾶς ἰούσης τε καὶ κρατουμένης, τὸ μὲν μείζονα αὐτῶν, τὸ δ’ ἐλάττω κύκλον ἰόν, θᾶττον μὲν τὰ τὸν ἐλάττω, τὰ δὲ τὸν μείζω βραδύτερον περιῄειν; (When all the heavenly bodies whose shared task it was to produce time had attained their appropriate movements, and when they had been generated as living beings, their bodies fastened with bonds of soul, and when each of them had understood its instructions, they began to revolve in conformity with the oblique movement of difference, which crosses the movement of identity and is subject to it. Their circles ranged from larger to smaller, and those with smaller circles revolved faster than those with larger circles which revolve more slowly); modified translation from Plato, Timaeus and Critias, trans. R. Waterfield (Oxford: Oxford University Press, 2008), 27.

² See De Caelo 291a29-34: Περὶ δὲ τῆς τάξεως αὐτῶν, ὃν μὲν τρόπον ἕκαστα κεῖται τῷ τὰ μὲν εἶναι πρότερα τὰ δ’ ὕστερα, καὶ πῶς ἔχει πρὸς ἄλληλα τοῖς ἀποστήμασιν, ἐκ τῶν περὶ ἀστρολογίαν θεωρείσθω· λέγεται γὰρ ἱκανῶς. Συμβαίνει δὲ κατὰ λόγον γίγνεσθαι τὰς ἑκάστου κινήσεις τοῖς ἀποστήμασι τῷ τὰς μὲν εἶναι θάττους τὰς δὲ βραδυτέρας; (“The questions of their order, their relative positions before or behind each other, and their distances from one another, may best be studied in astronomical writings, where they are adequately discussed. One characteristic is that their movements are faster or slower according to their distances”); Aristotle, On the Heavens, trans. W. K. C. Guthrie, Loeb Classical Library No. 338 (Cambridge, Massachusetts: Harvard University Press, 1939), II: 10, 291a29-34.

³ See B. R. Goldstein, “Copernicus and the Origin of his Heliocentric System,” Journal for the History of Astronomy 33, 3 (2002): 231; cf. A. Goddu, “Reflections on the Origin of Copernicus’s Cosmology,” Journal for the History of Astronomy 37, 1 (2006): 37-53; M. Vesel, Copernicus: Platonist Astronomer-Philosopher, Cosmic Order, the Movement of the Earth, and the Scientific Revolution (Bern: Peter Lang, 2014), 231.

⁴ See M. Capella, De nuptiis Philologiae et Mercurii VIII, § 857: Nam Venus Mercuriusque licet ortus occasusque cotidianos ostendant, tamen eorum circuli terras omnino non ambiunt, sed circa Solem laxiore ambitu circulantur. denique circulorum suorum centron in Sole constituunt (Now Venus and Mercury, although they have daily risings and settings, do not travel about the Earth at all; rather, they encircle the Sun in wider revolutions. The center of their orbits is set in the Sun); trans. W. Stahl, R. Johnson, E. Burge, Martianus Capella and the Seven Liberal Arts (New York & London: Columbia University Press, 1971), 333.

⁵ B. Eastwood, “Plato and Circumsolar Planetary Motion in the Middle Ages,” Archives d’Histoire Doctrinale et Littéraire du Moyen Âge 60 (1993): 7-26.

⁶ See M. Capella, De nuptiis Philologiae et Mercurii, VIII. § 858; cf. W. Stahl, R. Johnson, E. Burge, Martianus Capella and the Seven Liberal Arts, 223, 333.

⁷ The value adopted by Capella for the lunar orbit was either 406,010 stadia multiplied by 100 or 252,000 stadia multiplied by 100. I use the first one since Capella mentioned that value in De Astronomia; at any rate, this discrepancy does not affect my argument.

⁸ See M. Capella, De Nuptiis Philologiae et Mercurii, VIII, § 861 and §§ 879-886. 

⁹ See N. Swerdlow, “The Derivation and First Draft of Copernicus’s Planetary Theory: A Translation of the Commentariolus with Commentary,” Proceedings of the American Philosophical Society 117, no. 6 (1973): 423-512; cf. N. Copernicus, De Revolutionibus Orbium Coelestium, fol. 9b; On the Revolutions, trans. E. Rosen (Baltimore: The John Hopkins University Press, 1992 (originally published as volume 2 of Nicholas Copernicus: Complete works (Warsaw: Polish Scientific Publishers, 1978)), vol. 2, 21; cf. A. Athanasakis, “Copernicus, Nicolaus,” in Encyclopedia of Renaissance Philosophy, edited by M. Sgarbi (Cham: Springer, 2021).

---